Teoría de conjuntos

La teoría de conjuntos es una rama fundamental de las matemáticas que estudia las propiedades y relaciones entre colecciones de objetos, a los que llamamos conjuntos.

¿Qué es un conjunto?

Imagina una caja donde puedes guardar cualquier tipo de objetos: números, letras, personas, frutas, etc. Esa caja sería un conjunto, y los objetos que contiene serían sus elementos.

Características de los conjuntos:

• Bien definidos: Los elementos de un conjunto deben estar claramente especificados para que se pueda determinar si un objeto pertenece o no al conjunto.
• No repetición: Un elemento no puede aparecer más de una vez en un conjunto.
• Orden irrelevante: El orden en que se listan los elementos de un conjunto no importa.

Ejemplos de conjuntos:

• Conjunto de los números naturales: {1, 2, 3, 4, ...}
• Conjunto de las vocales: {a, e, i, o, u}
• Conjunto de los días de la semana: {lunes, martes, miércoles, jueves, viernes, sábado, domingo}

Formas de representar conjuntos:

• Por extensión: Listando todos los elementos entre llaves. Ejemplo: A = {1, 2, 3, 4}
• Por comprensión: Describiendo los elementos que cumplen una determinada propiedad. Ejemplo: B = {x | x es un número par menor que 10}

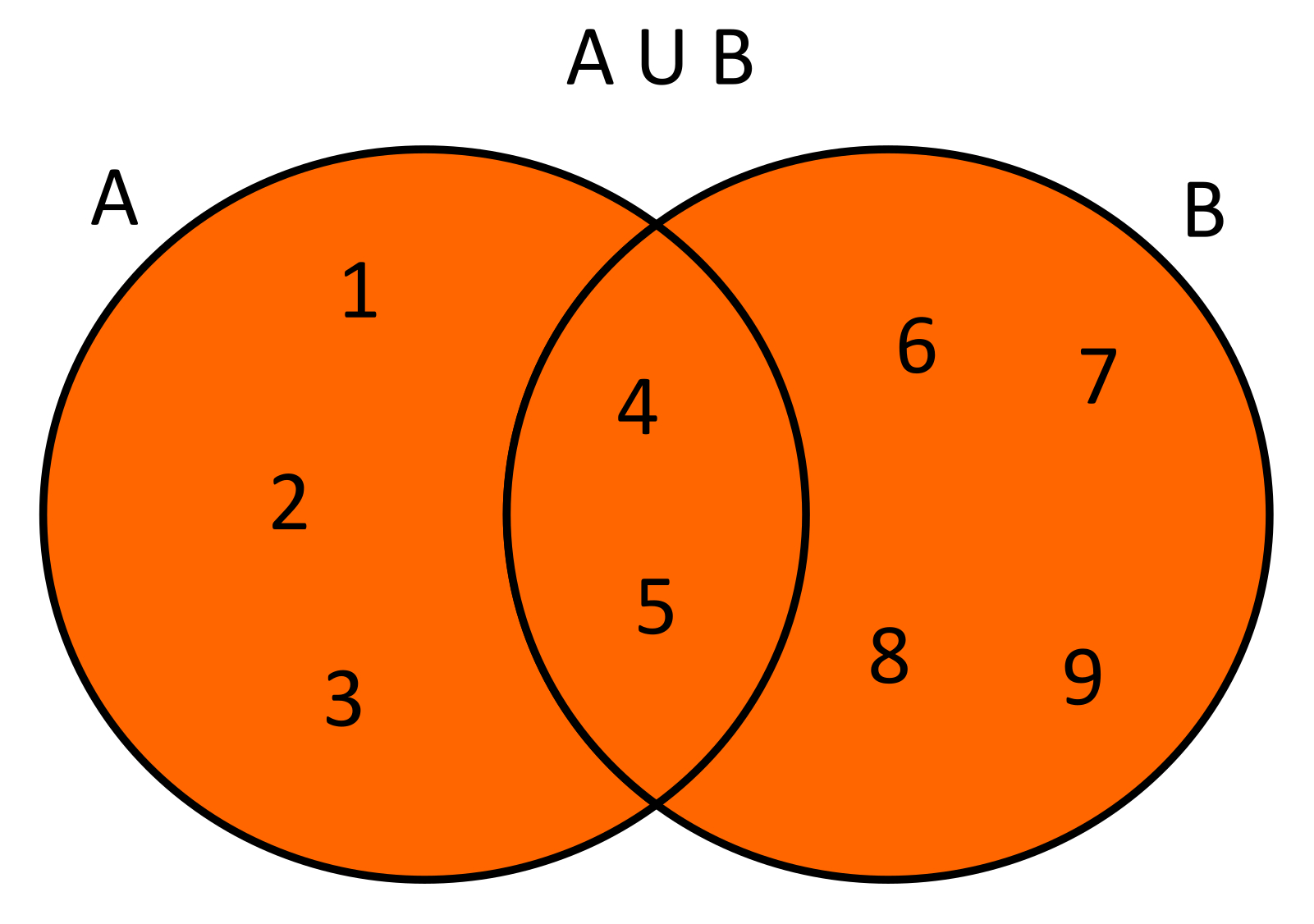
• Diagramas de Venn:

  Son una forma visual de representar conjuntos y sus relaciones. Utilizan círculos para representar los conjuntos y las zonas de solapamiento para mostrar las intersecciones.

Tipos de conjuntos:

• Conjunto vacío: No contiene ningún elemento. Se representa como ∅ o {}.
• Conjunto unitario: Contiene un solo elemento.
• Conjunto finito: Tiene un número determinado de elementos.
• Conjunto infinito: Tiene infinitos elementos.

Operaciones con conjuntos:

• Unión (∪): Combina todos los elementos de dos o más conjuntos.
  • Ejemplo: Si A = {1, 2, 3} y B = {3, 4, 5}, entonces A ∪ B = {1, 2, 3, 4, 5}.
• Intersección (∩): Contiene los elementos que pertenecen a ambos conjuntos.
  • Ejemplo: Si A = {1, 2, 3} y B = {3, 4, 5}, entonces A ∩ B = {3}.
• Diferencia (-): Contiene los elementos que pertenecen al primer conjunto pero no al segundo.
  • Ejemplo: Si A = {1, 2, 3} y B = {3, 4, 5}, entonces A - B = {1, 2}.
• Complemento (A'): Contiene todos los elementos que no pertenecen a un conjunto dado (dentro de un universo determinado).