Parábola
¿Qué es una Parábola?
Una parábola es una curva que se obtiene al cortar un cono con un plano paralelo a una de sus generatrices. Es una figura geométrica muy común en la naturaleza y en muchas aplicaciones de la ingeniería.
Características principales de una parábola:
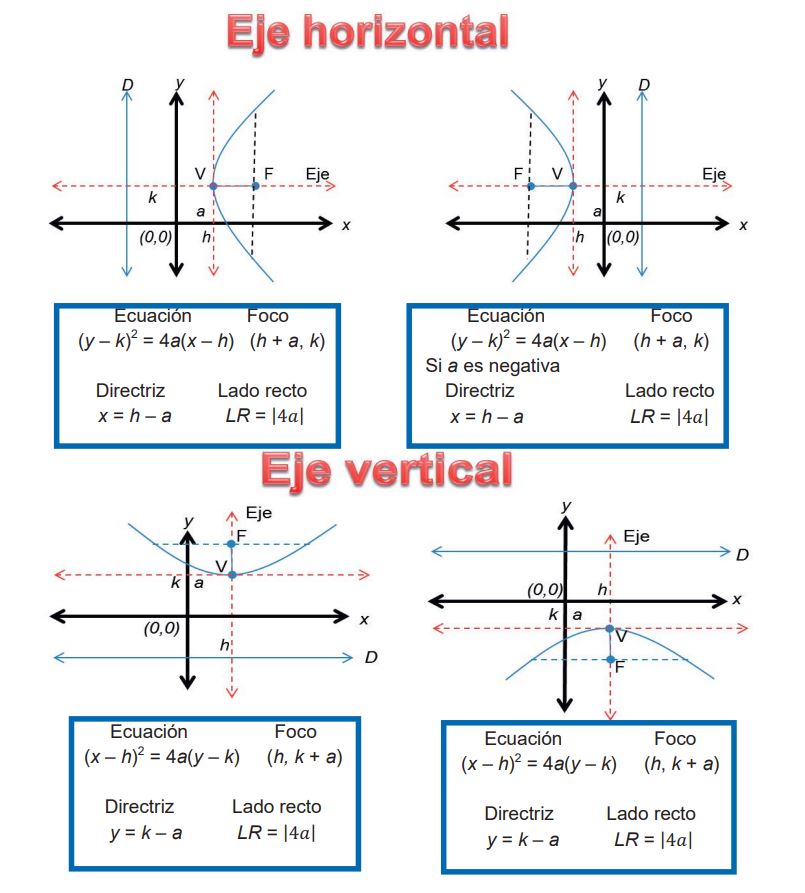
- Eje de simetría: Una línea recta que divide a la parábola en dos partes simétricas.
- Vértice: El punto donde la parábola interseca a su eje de simetría.
- Foco: Un punto fijo dentro de la parábola.
- Directriz: Una línea recta perpendicular al eje de simetría y ubicada a la misma distancia del vértice que el foco.
Ejercicio:
Encuentra el vértice, foco y directriz de la parábola cuya ecuación es:
y = -2(x + 1)² + 3
Solución paso a paso:
-
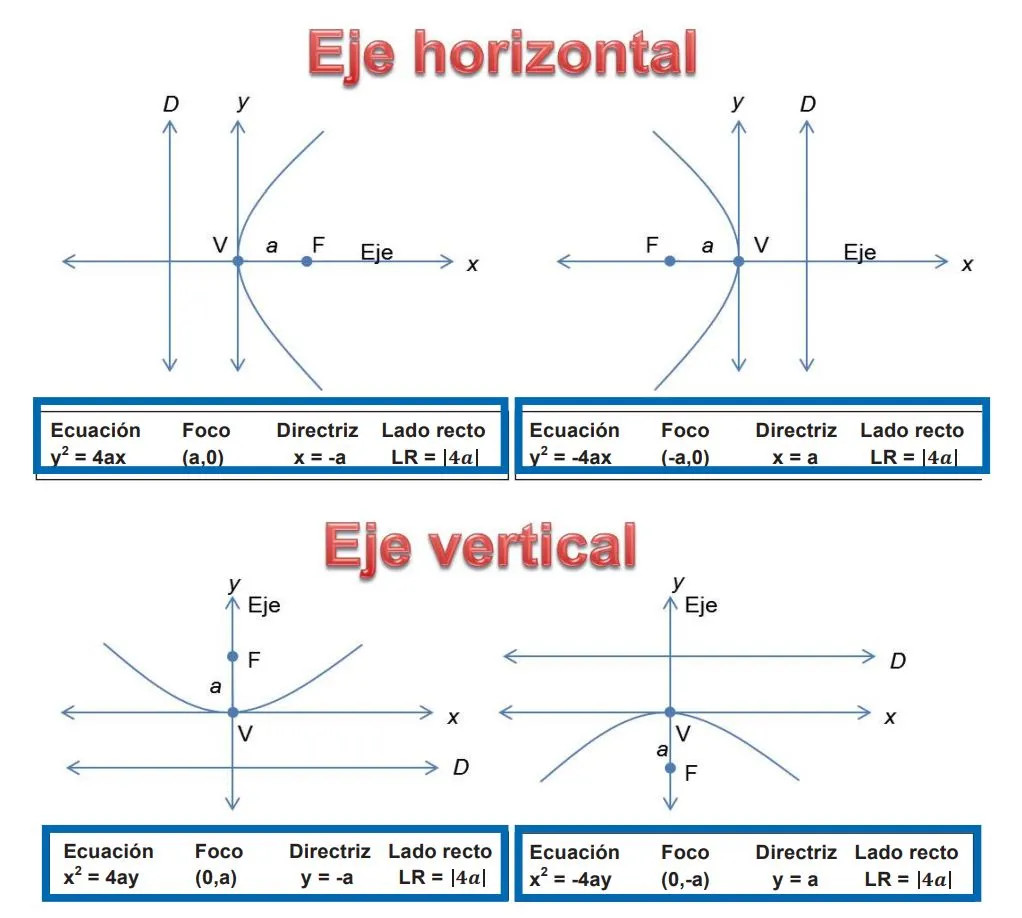
Identificar la forma estándar: La ecuación está en la forma estándar de una parábola con eje de simetría paralelo al eje y: y = a(x - h)² + k.
-
Comparar con la forma estándar: Al comparar, vemos que:
- a = -2
- h = -1
- k = 3
-
Encontrar el vértice: El vértice es el punto (h, k), por lo tanto, el vértice de esta parábola es (-1, 3).
-
Determinar la orientación: Como a = -2 < 0, la parábola se abre hacia abajo.
-
Encontrar el valor de p: El valor de p está relacionado con la distancia del vértice al foco y a la directriz. En este caso, p = 1 / (4|a|) = 1/8.
-
Encontrar el foco: Como la parábola se abre hacia abajo, el foco estará p unidades por debajo del vértice. Por lo tanto, el foco es (-1, 3 - 1/8) = (-1, 23/8).
-
Encontrar la directriz: La directriz es una línea horizontal que está a una distancia p por encima del vértice. Por lo tanto, la ecuación de la directriz es y = 3 + 1/8 = 25/8.
Respuesta:
- Vértice: (-1, 3)
- Foco: (-1, 23/8)
- Directriz: y = 25/8
Ejercicios relacionados
https://quizizz.com/join/quiz/5dd29b840f2a55001c992f5f/start?studentShare=true
Videos/paginas web que te ayudaran a la comprensión del tema:
https://www.universoformulas.com/matematicas/geometria/parabola/