operaciones con conjuntos
Las operaciones de conjuntos son acciones matemáticas que se realizan sobre conjuntos (colecciones de elementos) para formar nuevos conjuntos. Estas operaciones permiten combinar, relacionar y comparar diferentes conjuntos de elementos.
Operaciones Básicas
-
Unión (∪):
- Combina todos los elementos de dos o más conjuntos en un solo conjunto.
- Ejemplo: Si A = {1, 2, 3} y B = {3, 4, 5}, entonces A ∪ B = {1, 2, 3, 4, 5}.
-
Intersección (∩):
- Contiene los elementos que pertenecen a ambos conjuntos.
- Ejemplo: Si A = {1, 2, 3} y B = {3, 4, 5}, entonces A ∩ B = {3}.
-
Diferencia (-):
- Contiene los elementos que pertenecen al primer conjunto pero no al segundo.
- Ejemplo: Si A = {1, 2, 3} y B = {3, 4, 5}, entonces A - B = {1, 2}.
-
Complemento (A'):
- Contiene todos los elementos que no pertenecen a un conjunto dado (dentro de un universo determinado).
- Ejemplo: Si U = {1, 2, 3, 4, 5} es el universo y A = {1, 2, 3}, entonces A' = {4, 5}.
Propiedades de las Operaciones
- Conmutativa: La unión y la intersección son conmutativas, es decir, el orden de los conjuntos no altera el resultado.
- A ∪ B = B ∪ A
- A ∩ B = B ∩ A
- Asociativa: La unión y la intersección son asociativas, lo que significa que podemos agrupar los conjuntos de diferentes maneras sin cambiar el resultado.
- (A ∪ B) ∪ C = A ∪ (B ∪ C)
- (A ∩ B) ∩ C = A ∩ (B ∩ C)
- Distributiva: La unión y la intersección son distributivas una respecto a la otra.
- A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
- Universo: El conjunto de todos los posibles elementos que estamos considerando.
- Conjunto vacío: Un conjunto que no contiene ningún elemento. Se representa como ∅.
- Subconjunto: Un conjunto A es subconjunto de un conjunto B si todos los elementos de A también pertenecen a B. Se representa como A ⊆ B.
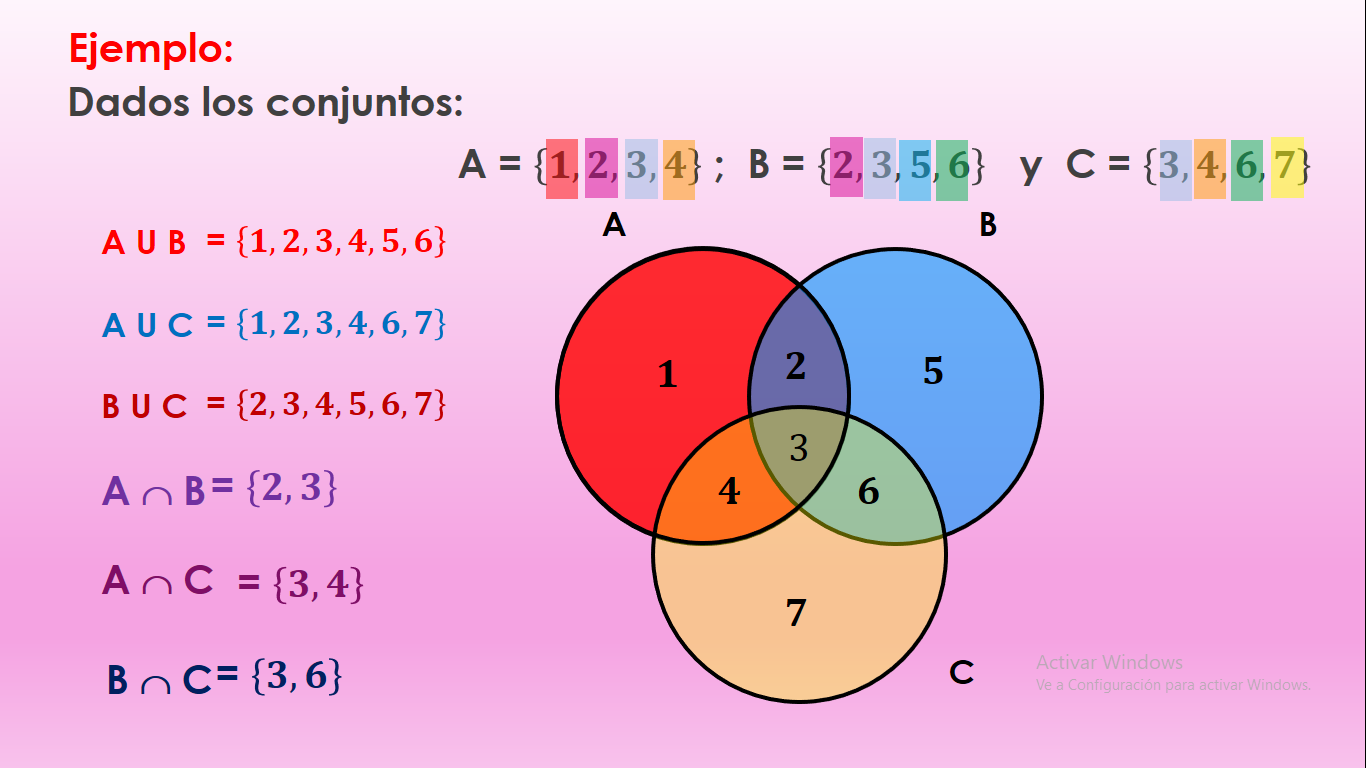
Ejemplo:
Imagina que tienes dos conjuntos:
A: {1, 2, 3}
B: {3, 4, 5}
Unión (A ∪ B): {1, 2, 3, 4, 5}
Intersección (A ∩ B): {3}
Diferencia (A - B): {1, 2}
Complemento de A (si el universo es {1, 2, 3, 4, 5}): {4, 5}
Ejercicio 1:
Dados los conjuntos:
- A = {1, 2, 3, 4}
- B = {3, 4, 5, 6}
Encuentra:
- A ∪ B
- A ∩ B
- A - B
- B - A
Respuestas:
- A ∪ B = {1, 2, 3, 4, 5, 6} (Todos los elementos de ambos conjuntos)
- A ∩ B = {3, 4} (Elementos comunes a ambos conjuntos)
- A - B = {1, 2} (Elementos en A pero no en B)
- B - A = {5, 6} (Elementos en B pero no en A)
Ejercicio 2:
Dado el universo U = {1, 2, 3, 4, 5, 6, 7, 8} y los conjuntos A = {1, 3, 5, 7} y B = {2, 4, 6, 8}, encuentra:
- A'
- B'
- (A ∪ B)'
Respuestas: Ejercicio 1
- A ∪ B = {1, 2, 3, 4, 5, 6} (Todos los elementos de ambos conjuntos)
- A ∩ B = {3, 4} (Elementos comunes a ambos conjuntos)
- A - B = {1, 2} (Elementos en A pero no en B)
- B - A = {5, 6} (Elementos en B pero no en A)
Respuestas: Ejercicio 2
- A' = {2, 4, 6, 8} (Elementos en U pero no en A)
- B' = {1, 3, 5, 7} (Elementos en U pero no en B)
- (A ∪ B)' = ∅ (El complemento de la unión de A y B es el conjunto vacío, ya que A ∪ B abarca todos los elementos del universo)
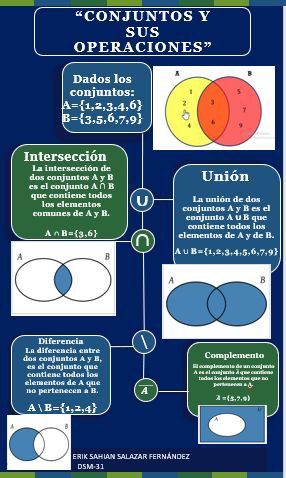
Ejercicios relacionados al tema
https://quizizz.com/join/quiz/602eb1f872d27c001d46fa01/start?studentShare=true
Videos que te ayudaran a la comprensión del tema
https://youtu.be/KmcRMlv9_T4?list=PLeySRPnY35dHACeGz_7oiU5Wo11AUt964