Funciones y relaciones
¿Qué es una función?
Una función es una relación entre dos conjuntos, llamada dominio y codominio, donde a cada elemento del dominio le corresponde un único elemento del codominio. Es decir, es una regla que asigna a cada valor de entrada (variable independiente) exactamente un valor de salida (variable dependiente).
Representación de una función:
Las funciones pueden representarse de diversas formas:
- Algebraicamente: Mediante una ecuación, como f(x) = 2x + 1.
- Gráficamente: Como una curva en un plano cartesiano.
- Tablas de valores: Listando pares ordenados (x, y), donde x pertenece al dominio e y es su imagen.
- Diagramas de flechas: Representando los elementos del dominio y codominio y las correspondencias entre ellos.
Elementos de una función:
- Dominio: Conjunto de todos los valores posibles de la variable independiente (x).
- Codominio: Conjunto de todos los posibles valores de la variable dependiente (y).
- Rango: Subconjunto del codominio que corresponde a las imágenes de los elementos del dominio.
Tipos de funciones:
Existen numerosos tipos de funciones, cada una con sus propias características:
- Funciones algebraicas: Polinómicas, racionales, irracionales.
- Funciones trascendentes: Exponenciales, logarítmicas, trigonométricas.
- Funciones a trozos: Definidas por diferentes expresiones en diferentes intervalos.
Propiedades de las funciones:
- Inyectiva: Cada elemento del codominio tiene a lo sumo una preimagen en el dominio.
- Sobreyectiva: Todo elemento del codominio tiene al menos una preimagen en el dominio.
- Biyectiva: La función es inyectiva y sobreyectiva a la vez.
Operaciones con funciones:
Las funciones se pueden sumar, restar, multiplicar, dividir y componer.
Aplicaciones de las funciones:
Las funciones tienen aplicaciones en prácticamente todas las áreas de la ciencia, ingeniería y economía. Se utilizan para modelar fenómenos físicos, analizar datos, optimizar procesos, etc.
Ejemplos de funciones:
- Función lineal: f(x) = mx + b
- Función cuadrática: f(x) = ax^2 + bx + c
- Función exponencial: f(x) = a^x
- Función logarítmica: f(x) = log_a(x)
- Función trigonométrica: f(x) = sen(x), cos(x), tan(x)
¿Qué es una relación?
Una relación es una correspondencia o vínculo entre los elementos de dos conjuntos. Es decir, nos indica cómo se relacionan los elementos de un conjunto con los elementos de otro.
Representación de una relación:
Existen varias formas de representar una relación:
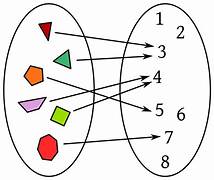
- Diagramas de Venn: Se utilizan círculos para representar los conjuntos y flechas para indicar las relaciones entre los elementos.
- Pares ordenados: Cada par ordenado (a, b) indica que el elemento a del primer conjunto está relacionado con el elemento b del segundo conjunto.
- Tablas: Se utilizan tablas para listar los pares ordenados de una relación.
- Gráficas: Se utilizan gráficos cartesianos para representar relaciones entre conjuntos de números reales.
Ejemplo:
Consideremos dos conjuntos: A = {1, 2, 3} y B = {a, b}. Una relación R entre A y B podría ser: R = {(1, a), (2, b), (3, a)}. Esto significa que 1 está relacionado con a, 2 con b y 3 con a.
Tipos de relaciones:
Existen diferentes tipos de relaciones, cada una con características particulares:
- Relación reflexiva: Todo elemento está relacionado consigo mismo.
- Relación simétrica: Si a está relacionado con b, entonces b está relacionado con a.
- Relación transitiva: Si a está relacionado con b y b está relacionado con c, entonces a está relacionado con c.
- Relación de equivalencia: Una relación que es reflexiva, simétrica y transitiva.
Relaciones y funciones:
Una función es un tipo especial de relación donde cada elemento del primer conjunto (dominio) está asociado con exactamente un elemento del segundo conjunto (codominio). Es decir, en una función, a cada entrada le corresponde una única salida.
Pasos generales para resolver problemas con funciones y relaciones:
- Identificar los conjuntos involucrados: Determina cuáles son los conjuntos de partida y llegada (dominio y codominio) de la relación o función.
- Analizar la correspondencia: Examina cómo se relacionan los elementos de un conjunto con los del otro. ¿Cada elemento tiene una única imagen?
- Representar la relación o función: Puedes usar diagramas de Venn, pares ordenados, tablas o gráficas para visualizar la relación.
- Determinar el dominio y rango: El dominio es el conjunto de todos los valores posibles de entrada, y el rango es el conjunto de todos los valores posibles de salida.
- Verificar si se cumplen las propiedades: Para las funciones, verifica si cada elemento del dominio tiene una única imagen. Para las relaciones, puedes analizar si son reflexivas, simétricas, transitivas, etc.
- Resolver problemas específicos: Dependiendo del problema, podrías necesitar evaluar la función en un punto, encontrar la inversa, determinar si es inyectiva, sobreyectiva o biyectiva, etc.
Ejemplo:
Problema: Dada la función f(x) = 2x + 1, encuentra f(3).
Solución:
- Identificamos que la función f toma un número x y le asigna el valor 2x + 1.
- Para encontrar f(3), simplemente sustituimos x por 3 en la expresión de la función: f(3) = 2(3) + 1 = 7.
Otro ejemplo:
Problema: Determina si la relación R = {(1,2), (2,3), (3,2)} definida en el conjunto A = {1, 2, 3} es una función.
Solución:
- La relación R relaciona elementos del conjunto A consigo mismos.
- Observamos que el elemento 2 aparece como imagen de 1 y de 3.
- Como un elemento del dominio (2) tiene dos imágenes diferentes (3 y 2), la relación R no es una función

Ejercicios relacionados
https://quizizz.com/join/quiz/604e64ccc83a6e001ebfe85f/start?studentShare=true
Videos que te podrían ayudar a su comprensión: